Single- and multi-qubit gate of varying complexity. More...
Public Member Functions | |
| Gate () | |
| Constructs the 2 × 2 zero matrix. | |
| Gate (const int rows, const int cols) | |
Constructs the rows × cols zero matrix. | |
| Gate & | operator= (const MatrixXc &m) |
| Gate | tensorDot (const Gate &m) const |
Computes the tensor product of this gate with m. | |
| Gate & | tensorDotSet (const Gate &m) |
Sets the tensor product of this gate and m as this gate. | |
| Gate | tensorPow (const int n) const |
Computes the nth tensor power of this gate. | |
| Gate & | tensorPowSet (const int n) |
Sets the nth tensor power of this gate as this gate. | |
| Gate | applyTo (const int j, const int n) const |
Extends this gate to a n-qubits gate. | |
| Gate & | applyToSet (const int j, const int n) |
Sets the to n-qubits extended gate as this gate. | |
| Gate & | X () |
X gate ( 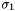 Pauli matrix, NOT gate) Pauli matrix, NOT gate) | |
| Gate & | Y () |
Y gate ( 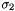 Pauli matrix) Pauli matrix) | |
| Gate & | Z () |
Z gate ( 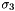 Pauli matrix) Pauli matrix) | |
| Gate & | H () |
| H gate (Hadamard gate) | |
| Gate & | P () |
| P gate (phase shift gate) | |
| Gate & | T () |
T gate ( 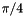 phase shift gate) phase shift gate) | |
| Gate & | R (const fptype k) |
R(k) gate (general phase shift gate) | |
| Gate & | I () |
| I gate (identity gate) | |
| Gate & | Rx (const fptype theta) |
Rx(theta) gate | |
| Gate & | Ry (const fptype theta) |
Ry(theta) gate | |
| Gate & | Rz (const fptype theta) |
Rz(theta) gate | |
| Gate & | CNOT () |
| CNOT gate (controlled NOT gate) | |
| Gate & | CCNOT () |
| CCNOT gate (Toffoli gate, controlled CNOT gate) | |
| Gate & | CSWAP () |
| CSWAP gate (Fredkin gate, controlled SWAP gate) | |
| Gate & | C (const int t, const int c, const int n, const Gate &U) |
Ctcn(U) gate (controlled U gate) | |
| Gate & | SWAP () |
| SWAP gate | |
| Gate & | S (const int p, const int q, const int n) |
Spqn gate | |
| Gate & | S (const std::vector< int > &sigma) |
S(sigma) gate | |
| Gate & | U (const std::vector< int > &f) |
| Uf gate for one output qubit | |
| Gate & | U (const std::vector< int > &f, const int m) |
| Uf gate for multiple output qubits | |
| Gate & | F (const int n) |
Fn gate (quantum Fourier transform (QFT) gate) | |
Single- and multi-qubit gate of varying complexity.
The Gate class is the base for all quantum circuits in QuCoSi. It provides common quantum gates for one to three qubits, more complex gates for an arbitrary number of qubits, and methods to combine or extend them. Since gates are represented by unitary matrices, this class is derived of Eigen's dynamic size matrix class that uses complex numbers. Therefore composition of multiple gates is easily accomplished by simple matrix multiplication of single gates.
Definition at line 42 of file Gate.
| QuCoSi::Gate::Gate | ( | ) | [inline] |
| QuCoSi::Gate::Gate | ( | const int | rows, | |
| const int | cols | |||
| ) | [inline] |
Sets the tensor product of this gate and m as this gate.
| m | the right hand side operand of the tensor product |
*this Definition at line 117 of file Gate.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| Gate QuCoSi::Gate::tensorPow | ( | const int | n | ) | const [inline] |
Computes the nth tensor power of this gate.
The nth tensor power of a gate 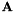 is the
is the n-fold tensor product of 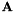 with itself:
with itself:
![\[ \mathbf{A}^{\otimes n} = \underbrace{\mathbf{A} \otimes \ldots \otimes \mathbf{A}}_n \ . \]](form_9.png)
| n | the exponent of the tensor power |
nth power Definition at line 136 of file Gate.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| Gate& QuCoSi::Gate::tensorPowSet | ( | const int | n | ) | [inline] |
Sets the nth tensor power of this gate as this gate.
| n | the exponent of the tensor power |
*this Definition at line 151 of file Gate.
 Here is the call graph for this function:
Here is the call graph for this function:| Gate QuCoSi::Gate::applyTo | ( | const int | j, | |
| const int | n | |||
| ) | const [inline] |
Extends this gate to a n-qubits gate.
This method constructs a gate that acts on n qubits so that the original gate acts on the qubit(s) at position j and all other qubits are left unchanged. This is accomplished by tensor multiplication of an appropriate number of identity gates from the left and the right to the original gate.
| j | the position of the qubit(s) the original gate acts on | |
| n | the number of qubits the returned gate acts on |
n qubits extended gate Definition at line 170 of file Gate.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| Gate& QuCoSi::Gate::applyToSet | ( | const int | j, | |
| const int | n | |||
| ) | [inline] |
| Gate& QuCoSi::Gate::X | ( | ) | [inline] |
| Gate& QuCoSi::Gate::Y | ( | ) | [inline] |
| Gate& QuCoSi::Gate::Z | ( | ) | [inline] |
| Gate& QuCoSi::Gate::H | ( | ) | [inline] |
| Gate& QuCoSi::Gate::P | ( | ) | [inline] |
| Gate& QuCoSi::Gate::T | ( | ) | [inline] |
| Gate& QuCoSi::Gate::I | ( | ) | [inline] |
| Gate& QuCoSi::Gate::CNOT | ( | ) | [inline] |
| Gate& QuCoSi::Gate::CCNOT | ( | ) | [inline] |
| Gate& QuCoSi::Gate::CSWAP | ( | ) | [inline] |
Ctcn(U) gate (controlled U gate)
This method constructs a gate that acts on n qubits so that the gate U is applied to the qubit(s) at position t (the target qubit(s)) if the qubit at position c (the control qubit) is 1.
| t | the position of the target qubit(s) | |
| c | the position of the control qubit | |
| n | the number of qubits this gate acts on | |
| U | the gate that acts on the target qubit and that is controlled by the control qubit |
*this Definition at line 537 of file Gate.
 Here is the call graph for this function:
Here is the call graph for this function:| Gate& QuCoSi::Gate::SWAP | ( | ) | [inline] |
| Gate& QuCoSi::Gate::S | ( | const int | p, | |
| const int | q, | |||
| const int | n | |||
| ) | [inline] |
Spqn gate
This method constructs a 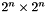 tensor permutation matrix that permutes the
tensor permutation matrix that permutes the pth and qth qubits in a tensor product of n qubits.
| p | the new position of the qth qubit | |
| q | the new position of the pth qubit | |
| n | the number of qubits this gate acts on |
*this Definition at line 609 of file Gate.
 Here is the caller graph for this function:
Here is the caller graph for this function:| Gate& QuCoSi::Gate::S | ( | const std::vector< int > & | sigma | ) | [inline] |
S(sigma) gate
This method constructs a tensor permutation matrix that permutes qubits according to the permutation sigma. For example, this matrix acts on the tensor product of the qubits 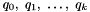 as follows:
as follows:
![\[ \mathbf{S}(\sigma) \left(q_0 \otimes q_1 \otimes \ldots \otimes q_k\right) = q_{\sigma(0)} \otimes q_{\sigma(1)} \otimes \ldots \otimes q_{\sigma(k)} \ . \]](form_31.png)
 and
and  can be obtained from the row and column indices of the permutation matrix with
can be obtained from the row and column indices of the permutation matrix with std::bitsets.| sigma | the permutation that will be applied to qubits |
*this | Gate& QuCoSi::Gate::U | ( | const std::vector< int > & | f | ) | [inline] |
Uf gate for one output qubit
This method constructs a gate that can be associated with the function 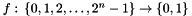 . It is defined so that it acts on a tensor product of n + 1 qubits as
. It is defined so that it acts on a tensor product of n + 1 qubits as
![\[ \mathbf{U}_f |x\rangle_n |y\rangle_1 = |x\rangle_n |y \oplus f(x)\rangle_1 \ , \]](form_35.png)
where 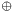 denotes binary addition.
denotes binary addition.
| f | the function associated with this gate |
*this | Gate& QuCoSi::Gate::U | ( | const std::vector< int > & | f, | |
| const int | m | |||
| ) | [inline] |
Uf gate for multiple output qubits
This method constructs a gate that can be associated with the function 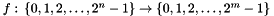 . It is defined so that it acts on a tensor product of n +
. It is defined so that it acts on a tensor product of n + m qubits as
![\[ \mathbf{U}_f |x\rangle_n |y\rangle_m = |x\rangle_n |y \oplus f(x)\rangle_m \ , \]](form_38.png)
where 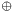 denotes bitwise binary addition.
denotes bitwise binary addition.
| f | the function associated with this gate | |
| m | the number of output qubits |
*this | Gate& QuCoSi::Gate::F | ( | const int | n | ) | [inline] |
 1.7.1
1.7.1